ANOVA Hypothesis Testing

jkesler

F Distribution and One-Way ANOVA

46 ANOVA Hypothesis Testing

[latexpage]

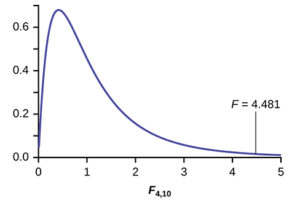
Here are some facts about the F distribution.

The curve is not symmetrical but skewed to the right.
There is a different curve for each set of df s.
The F statistic is greater than or equal to zero.
As the degrees of freedom for the numerator and for the denominator get larger, the curve approximates the normal.
Other uses for the F distribution include comparing two variances and two-way Analysis of Variance. Two-Way Analysis is beyond the scope of this chapter.

This graph has an unmarked Y axis and then an X axis that ranges from 0.00 to 4.00. It has three plot lines. The plot line labelled F subscript 1, 5 starts near the top of the Y axis at the extreme left of the graph and drops quickly to near the bottom at 0.50, at which point is slowly decreases in a curved fashion to the 4.00 mark on the X axis. The plot line labelled F subscript 100, 100 remains at Y = 0 for much of its length, except for a distinct peak between 0.50 and 1.50. The peak is a smooth curve that reaches about half way up the Y axis at its peak. The plot line labeled F subscript 5, 10 increases slightly as it progresses from 0.00 to 0.50, after which it peaks and slowly decreases down the remainder of the X axis. The peak only reaches about one fifth up the height of the Y axis.

Figure 11.3

Example 11.2

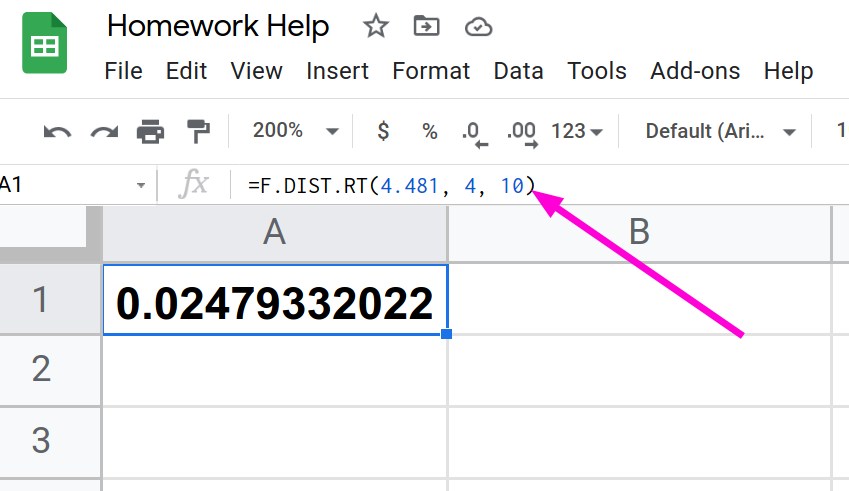
Let’s return to the slicing tomato exercise in Try It. The means of the tomato yields under the five mulching conditions are represented by μ₁, μ₂, μ₃, μ₄, μ₅. We will conduct a hypothesis test to determine if all means are the same or at least one is different. Using a significance level of 5%, test the null hypothesis that there is no difference in mean yields among the five groups against the alternative hypothesis that at least one mean is different from the rest.

Solution 11.2

The null and alternative hypotheses are:

H₀: μ₁ = μ₂ = μ₃ = μ₄ = μ₅

H₁: μ_i ≠ μ_j some i ≠ j

The one-way ANOVA results are shown in Figure 11.5

Source of Variation	Sum of Squares (SS)	Degrees of Freedom (df)	Mean Square (MS)	F
Factor (Between)	36,648,561	5 – 1 = 4	$\frac{36,648,561}{4}=9,162,140$	$\frac{9,162,140}{2,044,672.6}=4.481$
Error (Within)	20,446,726	15 – 5 = 10	$\frac{20,446,726}{10}=2,044,672.6$
Total	57,095,287	15 – 1 = 14

Table 11.5

Distribution for the test: F_4,10

df(num) = 5 – 1 = 4

df(denom) = 15 – 5 = 10

Test statistic: F = 4.4810

This graph shows a nonsymmetrical F distribution curve. The horizontal axis extends from 0 - 5, and the vertical axis ranges from 0 - 0.7. The curve is strongly skewed to the right.

Figure 11.4

Probability Statement: p-value = P(F > 4.481) = 0.0248. (see Google Sheets note below to find a p-value using a spreadsheet)

Compare α and the p-value: α = 0.05, p-value = 0.0248

Make a decision: Since α > p-value, we reject H₀.

Conclusion: At the 5% significance level, we have reasonably strong evidence that differences in mean yields for slicing tomato plants grown under different mulching conditions are unlikely to be due to chance alone. We may conclude that at least some of mulches led to different mean yields.

Finding P-values using Google Sheets

For ANOVA tests, use the F.DIST.RT formula with three arguments; the first is the F-test statistic, the second is the degrees of freedom between, and the third is the degrees of freedom within.

=F.DIST.RT(4.481, 4, 10)

Try It 11.2

MRSA, or Staphylococcus aureus, can cause a serious bacterial infections in hospital patients. Table 11.6 shows various colony counts from different patients who may or may not have MRSA. The data from the table is plotted in Figure 11.5.

Conc = 0.6	Conc = 0.8	Conc = 1.0	Conc = 1.2	Conc = 1.4
9	16	22	30	27
66	93	147	199	168
98	82	120	148	132

Table 11.6

Plot of the data for the different concentrations:

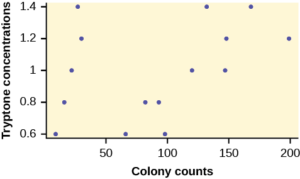
This graph is a scatterplot for the data provided. The horizontal axis is labeled 'Colony counts' and extends from 0 - 200. The vertical axis is labeled 'Tryptone concentrations' and extends from 0.6 - 1.4.

Figure 11.5

Test whether the mean number of colonies are the same or are different. Construct the ANOVA table, find the p-value, and state your conclusion. Use a 5% significance level.

Example 11.3

Four sororities took a random sample of sisters regarding their grade means for the past term. The results are shown in Table 11.7.

Sorority 1	Sorority 2	Sorority 3	Sorority 4
2.17	2.63	2.63	3.79
1.85	1.77	3.78	3.45
2.83	3.25	4.00	3.08
1.69	1.86	2.55	2.26
3.33	2.21	2.45	3.18

Table 11.7 MEAN GRADES FOR FOUR SORORITIES

Using a significance level of 1%, is there a difference in mean grades among the
sororities?

Solution 11.3

Let μ₁, μ₂, μ₃, μ₄ be the population means of the sororities. Remember that the null hypothesis claims that the sorority groups are from the same normal distribution. The alternate hypothesis says that at least two of the sorority groups come from populations with different normal distributions. Notice that the four sample sizes are each five.

Note

This is an example of a balanced design, because each factor (i.e., sorority) has the same number of observations.

H₀: μ₁ = μ₂ = μ₃ = μ₄

H₁: Not all of the means μ₁, μ₂, μ₃, μ₄ are equal.

Distribution for the test: F_3,16

where k = 4 groups and n = 20 samples in total

df(num)= k – 1 = 4 – 1 = 3

df(denom) = n – k = 20 – 4 = 16

Calculate the test statistic: F = 2.23

Graph:

Figure 11.6

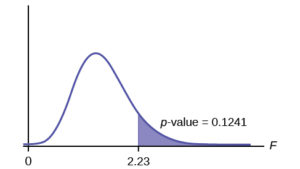
Probability statement: p-value = P(F > 2.23) = 0.1241 (find p-values using a spreadsheet like example 11.2)

Compare α and the p-value: α = 0.01
p-value = 0.1241
α < p-value

Make a decision: Since α < p-value, you cannot reject H₀.

Conclusion: There is not sufficient evidence to conclude that there is a difference among the mean grades for the sororities.

Try It 11.3

Four sports teams took a random sample of players regarding their GPAs for the last year. The results are shown in Table 11.8.

Basketball	Baseball	Hockey	Lacrosse
3.6	2.1	4.0	2.0
2.9	2.6	2.0	3.6
2.5	3.9	2.6	3.9
3.3	3.1	3.2	2.7
3.8	3.4	3.2	2.5

Table 11.8 GPAs FOR FOUR SPORTS TEAMS

Use a significance level of 5%, and determine if there is a difference in GPA among the teams.

Example 11.4

A fourth grade class is studying the environment. One of the assignments is to grow bean plants in different soils. Tommy chose to grow his bean plants in soil found outside his classroom mixed with dryer lint. Tara chose to grow her bean plants in potting soil bought at the local nursery. Nick chose to grow his bean plants in soil from his mother’s garden. No chemicals were used on the plants, only water. They were grown inside the classroom next to a large window. Each child grew five plants. At the end of the growing period, each plant was measured, producing the data (in inches) in Table 11.9.

Tommy’s Plants	Tara’s Plants	Nick’s Plants
24	25	23
21	31	27
23	23	22
30	20	30
23	28	20

Table 11.9

Does it appear that the three media in which the bean plants were grown produce the same mean height? Test at a 3% level of significance.

Solution 11.4

This time, we will perform the calculations that lead to the $F^\prime$ statistic. Notice that each group has the same number of plants, so we will use the formula $F^\prime = \frac{n\cdot s_{\bar x}^2}{s_\text{pooled}^2}$

First, calculate the sample mean and sample variance of each group.

	Tommy’s Plants	Tara’s Plants	Nick’s Plants
Sample Mean	24.2	25.4	24.4
Sample Variance	11.7	18.3	16.3

Table 11.10

Next, calculate the variance of the three group means (Calculate the variance of 24.2, 25.4, and 24.4). Variance of the group means = $s_\bar{x}^2 = 0.413$

Then MS_between = $n\cdot s_\bar{x}^2 = (5)(0.413)$ where n = 5 is the sample size (number of plants each child grew).

Calculate the mean of the three sample variances (Calculate the mean of 11.7, 18.3, and 16.3). Mean of the sample variances = 15.433 = s² pooled

Then MS_within = s²_pooled = 15.433.

The F statistic (or F ratio) is $F=\frac{MS_\text{between}}{MS_\text{within}}=\frac{n\cdot s_\bar{x}^2}{s_\text{pooled}^2}=\frac{(5)(0.413)}{15.433}=0.134$

The dfs for the numerator = the number of groups – 1 = 3 – 1 = 2.

The dfs for the denominator = the total number of samples – the number of groups = 15 – 3 = 12

The distribution for the test is F_2,12 and the F statistic is F = 0.134

The p-value is P(F > 0.134) = 0.8759. (find p-values using a spreadsheet like example 11.2)

Decision: Since α = 0.03 and the p-value = 0.8759, do not reject H₀.

Conclusion: With a 3% level of significance, from the sample data, the evidence is not sufficient to conclude that the mean heights of the bean plants are different.

Try It 11.4

Another fourth grader also grew bean plants, but this time in a jelly-like mass. The heights were (in inches) 24, 28, 25, 30, and 32. Do a one-way ANOVA test on the four groups. Are the heights of the bean plants different? Use the same method as shown in Example 11.4.

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Statistics with Google Sheets by jkesler is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Basketball	Baseball	Hockey	Lacrosse
3.6	2.1	4.0	2.0
2.9	2.6	2.0	3.6
2.5	3.9	2.6	3.9
3.3	3.1	3.2	2.7
3.8	3.4	3.2	2.5

Basketball	Baseball	Hockey	Lacrosse
3.6	2.1	4.0	2.0
2.9	2.6	2.0	3.6
2.5	3.9	2.6	3.9
3.3	3.1	3.2	2.7
3.8	3.4	3.2	2.5

Basketball	Baseball	Hockey	Lacrosse
3.6	2.1	4.0	2.0
2.9	2.6	2.0	3.6
2.5	3.9	2.6	3.9
3.3	3.1	3.2	2.7
3.8	3.4	3.2	2.5