Additional Information and Full Hypothesis Test Examples

jkesler

Hypothesis Testing with One Sample

35 Additional Information and Full Hypothesis Test Examples

[latexpage]

In a hypothesis test problem, you may see words such as “the level of significance is 1%.” The “1%” is the preconceived or preset α.
The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
If no level of significance is given, a common standard to use is α = 0.05.
When you calculate the p-value and draw the picture, the p-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
The alternative hypothesis, H₁, tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
H₁ never has a symbol that contains an equal sign.
Thinking about the meaning of the p-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller p-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p-value such as 0.4, as opposed to a p-value of 0.056 (alpha = 0.05 is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.

The following examples illustrate a left-, right-, and two-tailed test.

Example 8.11

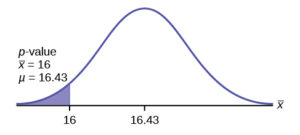
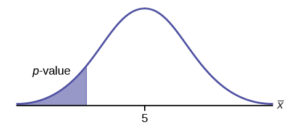
H_o: μ = 5, H₁: μ < 5

Test of a single population mean. H₁ tells you the test is left-tailed. The picture of the p-value is as follows:

Normal distribution curve of a single population mean with a value of 5 on the x-axis and the p-value points to the area on the left tail of the curve."

Figure 8.3

Try It 8.11

H₀: μ = 10, H₁: μ < 10

Assume the p-value is 0.0935. What type of test is this? Draw the picture of the p-value.

Example 8.12

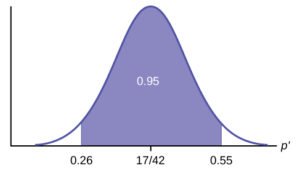
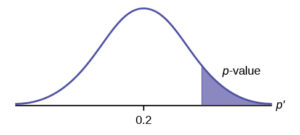
H₀: p = 0.2 H₁: p > 0.2

This is a test of a single population proportion. H₁ tells you the test is right-tailed. The picture of the p-value is as follows:

Normal distribution curve of a single population proportion with the value of 0.2 on the x-axis. The p-value points to the area on the right tail of the curve.

Figure 8.4

Try It 8.12

H₀: μ = 1, H₁: μ > 1

Assume the p-value is 0.1243. What type of test is this? Draw the picture of the p-value.

Example 8.13

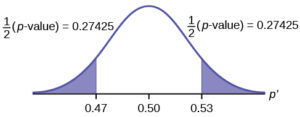
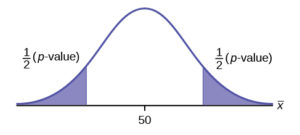
H₀: p = 50 H₁: p ≠ 50

This is a test of a single population mean. H₁ tells you the test is two-tailed. The picture of the p-value is as follows.

Normal distribution curve of a single population mean with a value of 50 on the x-axis. The p-value formulas, 1/2(p-value), for a two-tailed test is shown for the areas on the left and right tails of the curve.

Figure 8.5

Try It 8.13

H₀: p = 0.5, H₁: p ≠ 0.5

Assume the p-value is 0.2564. What type of test is this? Draw the picture of the p-value.

Full Hypothesis Test Examples

Example 8.14

Jeffrey, as an eight-year old, was bragging to his friends that his average time to swim the 25-yard freestyle is less than 16.43 seconds. His friends timed his next 15 25-yard freestyle swims. For the 15 swims, Jeffrey’s mean time was 16 seconds and his standard deviation was 0.8 seconds. Can Jeffery really claim that his average swim time is less than 16.43 seconds? Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.

Solution 8.14

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean.

H₀: μ = 16.43 H₁: μ < 16.43

For Jeffrey to swim faster, his time will be less than 16.43 seconds. The “<” tells you this is left-tailed.

Determine the distribution needed:

Random variable: $\bar X$ = the mean time to swim the 25-yard freestyle.

Distribution for the test: $\bar X$ is student-t (population standard deviation is unknown; only the sample standard deviation is known)

$\bar X \sim t_{df}\left( \mu \frac{\sigma_{X}}{\sqrt{n}} \right)$ Therefore, $\bar X \sim t_{14}\left(16.43 \frac{0.8}{\sqrt{15}} \right)$

μ = 16.43 comes from H₀ and not the data. σ = 0.8, and n = 15 so df = n-1 = 14.

Calculate the p-value using the t distribution for a mean:

p-value = $P(\bar x < 16) = 0.0281$ where the sample mean in the problem is given as 16. (See below for how to calculate this using Google Sheets).

p-value = 0.0281 (This is called the actual level of significance.) The p-value is the area to the left of the sample mean is given as 16.

Graph:

Normal distribution curve for the average time to swim the 25-yard freestyle with values 16, as the sample mean, and 16.43 on the x-axis. A vertical upward line extends from 16 on the x-axis to the curve. An arrow points to the left tail of the curve.

Figure 8.6

μ = 16.43 comes from H₀. Our assumption is μ = 16.43.

Interpretation of the p-value: If H₀ is true, there is a 0.0281 probability (2.81%)that Jeffrey’s mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It would be a rare event (if H₀ is true)

Compare α and the p-value:

α = 0.05 and p-value = 0.0281, so α > p-value

Make a decision: Since α > p-value, reject H₀.

This means that you reject μ = 16.43. In other words, you do not think Jeffrey swims the
25-yard freestyle in 16.43 seconds, but you do think he swims faster than 16.43 seconds.

Conclusion: At the 5% significance level, we conclude that Jeffrey swims faster than 16.43 seconds. The sample data show there is sufficient evidence that Jeffrey’s mean time to swim the 25-yard freestyle is less than 16.43 seconds.

The p-value can easily be calculated.

Using Google Sheets

In a cell, type

=TDIST( ABS( (16-16.43) / (0.8/SQRT(15) ) ), 14, 1)

The first value of the TDIST function is the positive version of the test statistic (TDIST requires a positive test statistic) calculated as $\frac{16-16.43}{0.8/\sqrt{15}}$ and wrapped in the ABS function (short for absolute value) to force it positive.

The second value given to the TDIST function is the degrees of freedom.

The third value given to the TDIST function is whether this is a 1-tail or 2-tail test.

The Type I and Type II errors for this problem are as follows:

The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on
average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)

The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard free-style, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)

Try It 8.14

The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards with a standard deviation of two yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.

First, determine what type of test this is, set up the hypothesis test, find the p-value, sketch the graph, and state your conclusion.

Historical Note (Example 8.11)

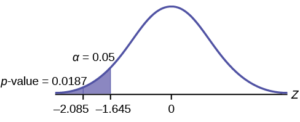
The traditional way to compare the two probabilities, α and the p-value, is to compare the critical value (z-score from α) to the test statistic (z-score from data). The calculated test statistic for the p-value is –2.08. (From the Central Limit Theorem, the test statistic formula is $z=\frac{\bar x -\mu_{X}}{\left(\frac{s_{X}}{\sqrt{n}}\right)}$

For this problem, $\bar x = 16$, μ_X = 16.43 from the null hypothes is, s_X = 0.8, and n = 15.) You can find the critical value for α = 0.05 in the student-t table. The t-score for an area to the left equal to 0.05 and degrees of freedom 14 is -1.761. Since –1.761 > –2.08 (which demonstrates that α > p-value), reject H₀. Traditionally, the decision
to reject or not reject was done in this way. Today, comparing the two probabilities α and the p-value is very common. For this problem, the p-value, 0.0281 is considerably smaller than α, 0.05. You can be confident about your decision to reject. The graph shows α, the p-value, and the test statistic and the critical value.

Distribution curve comparing the α to the p-value. Values of -2.15 and -1.645 are on the x-axis. Vertical upward lines extend from both of these values to the curve. The p-value is equal to 0.0158 and points to the area to the left of -2.15. α is equal to 0.05 and points to the area between the values of -2.15 and -1.645.

Figure 8.7

Example 8.15

A college football coach claims mean weight that his players can bench press is more than 275 pounds. His players wanted to test that claim. They asked 30 of their teammates for their estimated maximum lift on the bench
press exercise. The data ranged from 205 pounds to 385 pounds. The actual reported weights are listed in the table below:

205	225	265	316	341
205	241	275	316	345
205	241	275	316	345
215	252	313	316	368
215	252	313	338	368
215	265	316	338	385

Table 8.15

Conduct a hypothesis test using a 2.5% level of significance to determine if the bench press mean is more than 275 pounds.

Solution 8.15

Set up the Hypothesis Test:

Since the problem is about a mean weight, this is a test of a single population mean.

H₀: μ = 275
H₁: μ > 275
This is a right-tailed test.

Calculating the distribution needed:

Random variable: $\bar X$= the mean weight, in pounds, lifted by the football players.

Distribution for the test: It is a t distribution with 29 degrees of freedom (the sample size is 30)

$\bar X \sim t_{29}\left( 275, \frac{55}{\sqrt{30}} \right)$

$\bar x = 286.2$ pounds (from the data).

The sample’s standard deviation is s = 55.898 pounds (Use a spreadsheet to calculate this after importing the weight data). We assume μ = 275 pounds unless our data shows us otherwise.

Calculate the p-value using the t distribution with df=29 for a mean and using the sample mean $\bar x = 286.17$ as input $p -value = P (\bar{x} > 286.2) = 0.1323$

The test statistic is $t=\frac{\bar x -\mu}{s/\sqrt{n}}=\frac{286.17-275}{55.898/\sqrt{30}} = 1.095$

p-value= $P(\bar x > 286.17) = P(t>1.095) = 0.1413$

Interpretation of the p-value: If H₀ is true, then there is a 0.1413 probability (14.13%) that the football players can lift a mean weight of 286.17 pounds or more. Because a 14.13% chance is large enough, a mean weight lift of 286.17 pounds or more is not a rare event.

Compare α and the p-value:

α = 0.025 p-value = 0.1413

Make a decision: Since α <p-value, do not reject H₀.

Conclusion: At the 2.5% level of significance, from the sample data, there is not sufficient evidence to conclude that the true mean weight lifted is more than 275 pounds.

The p-value can easily be calculated.

Using Google Sheets

In a cell, type

=TDIST( ABS( (286.17-275) / (55.898 / SQRT(30) ) ), 29, 1 )

The first value give to the TDIST function is the positive version of our test statistic; the ABS function is unnecessary here because our test statistic is positive, but it is a good habit since the TDIST function will give an error if a negative test statistic is given.

The second value is the degrees of freedom, and the third value is the number of tails.

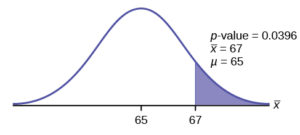
Example 8.16

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores

65
65
70
67
66
63
63
68
72
71

He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Solution 8.16

Set up the hypothesis test:

A 5% level of significance means that α = 0.05. This is a test of a single population mean.

H₀: μ = 65 H₁: μ > 65

Since the instructor thinks the average score is higher, use a “>”. The “>” means the test is right-tailed.

Determine the distribution needed:

Random variable: $\bar{X}$

$\bar X$= average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given. You are only given n = 10 sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student’s t.

Use t_df. Therefore, the distribution for the test is t₉ where n = 10 and df = 10 – 1 = 9.

Calculate the p-value using the Student’s t-distribution:

p-value = $P(\bar x >67) = 0.0396$ where the sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data (using a spreadsheet).

Interpretation of the p-value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

Normal distribution curve of average scores on the first statistic tests with 65 and 67 values on the x-axis. A vertical upward line extends from 67 to the curve. The p-value points to the area to the right of 67.

Figure 8.9

Compare α and the p-value:

Since α = 0.05 and p-value = 0.0396. α > p-value.

Make a decision: Since α > p-value, reject H₀.

This means you reject μ = 65. In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The p-value can easily be calculated.

Using Google Sheets

In a cell, type

=TDIST( ABS( (65-67) / (3.1972 / SQRT(10) ) ), 9, 1 )

The first value give to the TDIST function is the positive version of our test statistic; the ABS function is unnecessary here because our test statistic is positive, but it is a good habit since the TDIST function will give an error if a negative test statistic is given.

The second value is the degrees of freedom, and the third value is the number of tails.

Try It 8.16

It is believed that a stock price for a particular company will grow at a rate of \$5 per week with a standard deviation of \$1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: \$4, \$3, \$2, \$3, \$1, \$7, \$2, \$1, \$1, \$2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p-value, state your conclusion, and identify the Type I and Type II errors.

Example 8.17

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50%. Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of
significance.

Solution 8.17

Set up the hypothesis test:

The 1% level of significance means that α = 0.01. This is a test of a single population proportion.

H₀: p = 0.50 H₁: p ≠ 0.50

The words “is the same or different from” tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: $\hat P$ = the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The
information is given in terms of percentages. Use the distribution for $\hat P$, the estimated proportion.

$\hat P \sim N\left( p, \sqrt{\frac{pq}{n}} \right)$ Therefore, $\hat P \sim N\left( 0.5, \sqrt{\frac{(0.5)(0.5)}{100}} \right)$

where p = 0.50, q = 1−p = 0.50, and n = 100

Calculate the p-value using the normal distribution for proportions:

p-value = P ($\hat p$ < 0.47 or $\hat p$ > 0.53) = 0.5485

where x = 53, $\hat p =\frac{x}{n} =\frac{53}{100}=0.53$

Interpretation of the p-value: If the null hypothesis is true, there is 0.5485 probability
(54.85%) that the sample (estimated) proportion $\hat p$ is 0.53 or more OR 0.47 or less (see
the graph in Figure 8.10).

Normal distribution curve of the percent of first time brides who are younger than the groom with values of 0.47, 0.50, and 0.53 on the x-axis. Vertical upward lines extend from 0.47 and 0.53 to the curve. 1/2(p-values) are calculated for the areas on outsides of 0.47 and 0.53.

Figure 8.10

μ = p = 0.50 comes from H₀, the null hypothesis.

$\hat p$ = 0.53. Since the curve is symmetrical and the test is two-tailed, the $\hat p$ for the left tail is equal to 0.50 – 0.03 = 0.47 where μ = p = 0.50. (0.03 is the difference between 0.53 and 0.50.)

Compare α and the p-value:

Since α = 0.01 and p-value = 0.5485. α < p-value.

Make a decision: Since α < p-value, you cannot reject H₀.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

The p-value can easily be calculated.

Using Google Sheets

In a cell, type

=2*(1- NORM.S.DIST((0.53-0.5)/SQRT(0.5*0.5/100) ) )

This function starts with “2*” since we are performing a two tail test, we need to double our p-value.

Then, we have “1 – ” because we want to are to the right of 0.53; even though this is a two tail test, we know to calculate the area into the right tail beyond 0.53 because 0.53 is further to the right than 0.50 from our null hypothesis.

In our NORM.S.DIST function, we calculate our test statistic as $\frac{\bar x – \mu }{\sqrt{\frac{pq}{n}}}=\frac{0.53 – 0.5 }{\sqrt{\frac{(0.5)(0.5)}{100}}}$. The NORM.S.DIST function will give us the area to the left, but, as mentioned, we want the are to the right, which is why we subtract this from 1.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Try It 8.17

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the p-value, sketch the graph, and state your conclusion.

Example 8.18

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

Solution 8.18

Set up the Hypothesis Test:

H₀: p = 0.30 H₁: p ≠ 0.30

Determine the distribution needed:

The random variable is $\hat P$ = proportion of households that have three cell phones.

The distribution for the hypothesis test is $\hat P \sim N\left( 0.3, \sqrt{\frac{(0.3)(0.7)}{150}} \right)$

Now lets complete the following list:

The value that helps determine the p-value is $\hat p$. Calculate $\hat p$.
What is a success for this problem?
What is the level of significance?
Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.
Calculate the p-value.
Make a decision. _____________(Reject/Do not reject) H₀ because____________.

Answers:

$\hat p = \frac{x}{n}$ where x is the number of successes and n is the total number in the sample.
x = 43, n = 150
$\hat p =\frac{43}{150}$
A success is having three cell phones in a household.
The level of significance is the preset α. Since α is not given, assume that α = 0.05.
p-value = 0.7216
Assuming that α = 0.05, α < p-value. The decision is do not reject H₀ because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Try It 8.18

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p-value, state your conclusion, and identify the Type I and Type II errors.

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter p. The distribution for the test is normal. The estimated proportion $\hat p$ is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived α = 0.01, for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

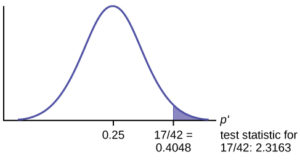
Example 8.19

My dog has so many fleas,

They do not come off with ease.

As for shampoo, I have tried many types

Even one called Bubble Hype,

Which only killed 25% of the fleas,

Unfortunately I was not pleased.

I’ve used all kinds of soap,

Until I had given up hope

Until one day I saw

An ad that put me in awe.

A shampoo used for dogs

Called GOOD ENOUGH to Clean a Hog

Guaranteed to kill more fleas.

I gave Fido a bath

And after doing the math

His number of fleas

Started dropping by 3’s!

Before his shampoo

I counted 42.

At the end of his bath,

I redid the math

And the new shampoo had killed 17 fleas.

So now I was pleased.

Now it is time for you to have some fun

With the level of significance being .01,

You must help me figure out

Use the new shampoo or go without?

Solution 8.19

Set up the hypothesis test:

H₀: p ≤ 0.25 H₁: p > 0.25

Determine the distribution needed:

In words, CLEARLY state what your random variable $\bar X$ or $\hat P$ represents.

$\hat P$ = The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

Normal:$N\left( 0.25, \sqrt{\frac{(0.25)(1-0.25)}{42}} \right)$

Test Statistic: z = 2.3163

Calculate the p-value using the normal distribution for proportions:

p-value = 0.0103

In one to two complete sentences, explain what the p-value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is $0.4048 \left( \frac{17}{42} \right) $ or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and
shade the region(s) corresponding to the p-value.

Normal distribution graph of the proportion of fleas killed by the new shampoo with values of 0.25 and 0.4048 on the x-axis. A vertical upward line extends from 0.4048 to the curve and the area to the left of this is shaded in. The test statistic of the sample proportion is listed.

Figure 8.11

Compare α and the p-value:

Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

alpha	decision	reason for decision
0.01	Do not reject H₀	α < p-value

Table 8.3

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation.
Label the point estimate and the lower and upper bounds of the confidence interval.

Normal distribution graph of the proportion of fleas killed by the new shampoo with values of 0.26, 17/42, and 0.55 on the x-axis. A vertical upward line extends from 0.26 and 0.55. The area between these two points is equal to 0.95.

Figure 8.12

Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

Note

This test result is not very definitive since the p-value is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example 8.20

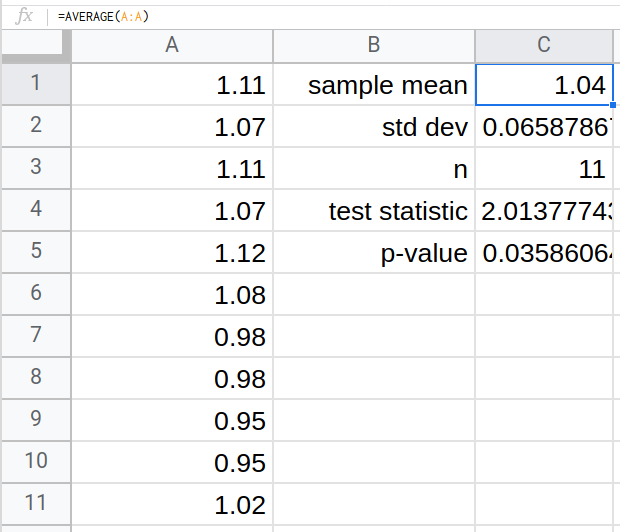
The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Solution 8.20

Let’s follow a four-step process to answer this statistical question.

State the Question: We need to determine if, at a 0.05 significance level, the average conductivity of the selected glass is greater than one. Our hypotheses will be
1. H₀: μ ≤ 1
2. H₁: μ > 1
Plan: We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student’s t-distribution. Assume the underlying population is normal.
Do the calculations: We will input the sample data into Google Sheets column A and calculate the p-value as follows:

Figure 8.13

Now that the data is in column A, we’ll calculate the mean, standard deviation, sample size (n), then we can calculate the test statistic and p-value. First create labels in column B for each of these.

Figure 8.14

In column C, enter the formulas to calculate each of the values.

In cell C1: =AVERAGE(A:A) to calculate the mean of all the data in column A.

In cell C2: =STDEV.S(A:A) to calculate the standard deviation of all the data in column A.

In cell C3: =COUNT(A:A) to count the number of data (sample size) in column A.

In cell C4: =(C1-1) / (C2 / SQRT(C3) ) to calculate the test statistic $t=\frac{\bar x -\mu}{s/\sqrt{n}}$ with $\mu =1$

In cell C5: =TDIST( ABS(C4), C3–1 , 1) to calculate the p-value, which is the area to the right of the positive version of our test statistic (TDIST requires a positive test statistic, so we use the ABS function to force the ABSolute value of our test statistic). We also input C3-1 degrees of freedom, and finally 1 tail.

Figure 8.15
State the Conclusions: Since the p-value (p = 0.036) is less than our alpha value (0.05), we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

Example 8.21

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

Solution 8.21

We will follow the four-step process.

We need to conduct a hypothesis test on the claimed cancer rate. Our hypotheses will be
1. H₀: p ≤ 0.00034
2. H₁: p > 0.00034
If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.
We will be testing a sample proportion with x = 172 and n = 420,019. The sample is sufficiently large because we have np = 420,019(0.00034) = 142.8, nq = 420,019(0.99966) = 419,876.2, two independent outcomes, and a fixed probability of success p = 0.00034. Thus we will be able to generalize our results to the population.
The associated Google Sheets results are
For the $\hat p$ (p-hat) calculation, use
=172/420019For the test statistic calculation, use
=(B1 - 0.00034) / SQRT(0.00034*0.99966/420019)For the p-value, use
=1-NORM.S.DIST(B2)
We subtract from 1 since this is a right tail test.
Since the p-value = 0.0073 is greater than our alpha value = 0.005, we cannot reject the null. Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example 8.22

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

Solution 8.22

We will follow the four-step plan.

We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
Since we are presented with proportions, we will use a one-proportion z-test. The hypotheses for the test will be
1. H₀: p = 0.00078
2. H₁: p ≠ 0.00078
The following screen shots display the summary statistics from the hypothesis test.

Figure 8.19

For the $\hat p$ (p-hat) calculation, use
=11/37937

For the test statistic calculation, use
=(B1 - 0.00078) / SQRT(0.00078*0.99922/37937)For the p-value, use
=2*NORM.S.DIST(B2)
We multiply by 2 since this is a 2-tail test.
Since the p-value, p = 0.00063, is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis. In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Statistics with Google Sheets by jkesler is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

205	225	265	316	341
205	241	275	316	345
205	241	275	316	345
215	252	313	316	368
215	252	313	338	368
215	265	316	338	385

205	225	265	316	341
205	241	275	316	345
205	241	275	316	345
215	252	313	316	368
215	252	313	338	368
215	265	316	338	385

205	225	265	316	341
205	241	275	316	345
205	241	275	316	345
215	252	313	316	368
215	252	313	338	368
215	265	316	338	385